Proposal: Add radix sort to std lib

[mzaks (Maxim)]

I have a repo which is a playground for different sorting algorithms.

GitHub - mzaks/mojo-sort

Radix sort is a specialized sorting algorithm which when used for appropriate use cases can provide very high performance benefits.

Please have a look at following benchmark: mojo-sort/benchmark_scalar_large_sort.mojo at main · mzaks/mojo-sort · GitHub

And corresponding report on MacBook Pro M4 Max: mojo-sort/scalar_large_report_m4.csv at main · mzaks/mojo-sort · GitHub

And a laptop with Zen 5 CPU: mojo-sort/scalar_large_report_zen5.csv at main · mzaks/mojo-sort · GitHub

As you can see the speed up factor varies from 4x to 36x.

Hence I want to propose to include Radix sort algorithm in Mojo standard library.

[owenhilyard]

nit: take Span instead of List

I think it would be nice to be able to radix sort things aside from SIMD types. Would it be possible to move some of the impl out to a trait so this generalizes?

One other thing I’d like to see the primitive used for is that I’ve seen radix sort used to minimize the amount of comparisons of another algorithm by sorting each of the buckets using a different key function or by making each bucket a heap. This can also help cut down on the number of buckets.

I think that it might also make sense to break out some parts of this to a reusable unordered hash map primitive, potentially with specializations for numeric types.

This allocating a fairly significant amount of memory also makes it a poor choice for hot loop code, could you expose a variant that passes in memory for the intermediate allocations, and then wrap that for the “nice” version?

[mzaks (Maxim)]

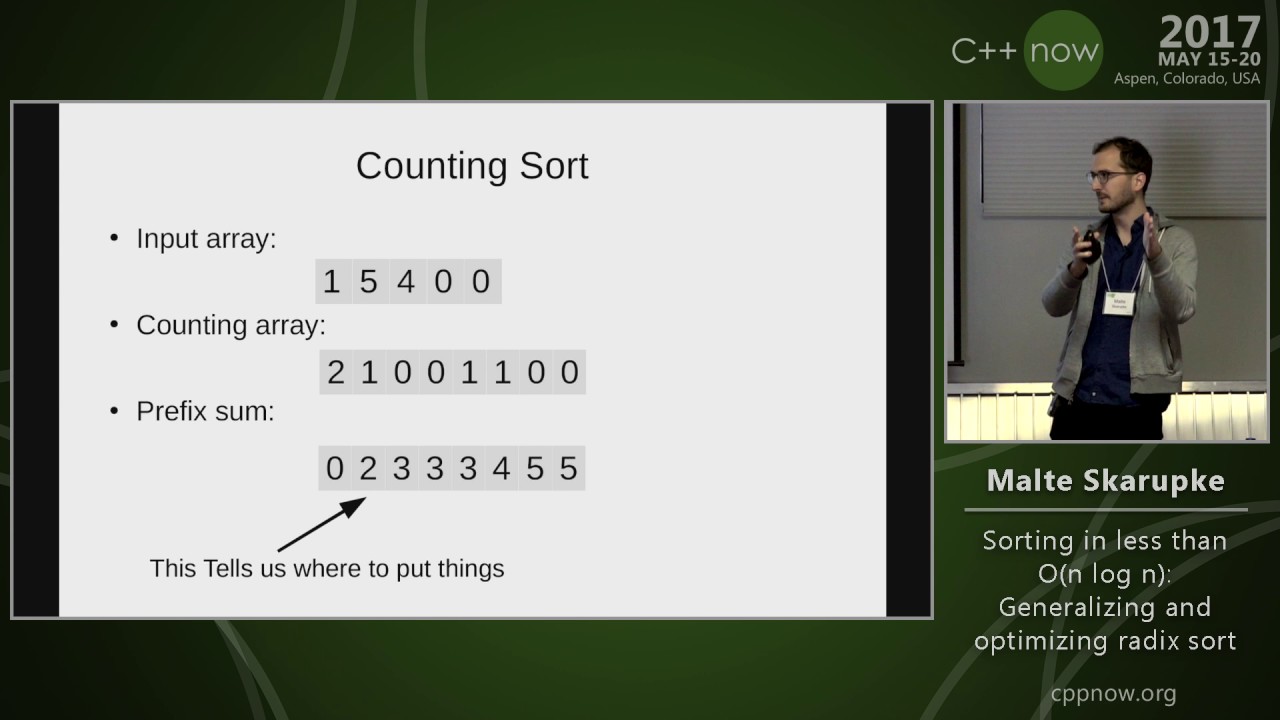
Based on your questions I watched this talk:

C++Now 2017: M. Skarupke “Sorting in less than O(n log n): Generalizing and optimizing radix sort"

Which kind of send me back to the drawing board

The radix sort I implemented is a “generic” copying LSB Radix sort for Scalar values, I do handle uint, int, and float, hence I call it generic, but it is not like you can sort any kind of data with it, just scalar numbers.

Radix11/13/16 is an alternative implementation based on this article stereopsis : graphics : radix tricks which is also a copying LSB Radix sort, with different computation of histogram (making it wider 11, 13, or 16 bits instead of 8), all the histograms are computed at the same time, the counts/offsets per bucket are computed a bit differently than the standard prefix sum and the temp memory is 2x compared to the typical Radix sort.

When we take a look at the benchmark report we can see that the Radix11 can be about 2x faster than my generic radix sort (Keep in mind that Radix11 only works on 32bit wide numbers). And the Radix13/16 variant (which wokrs on 64bit wide numbers) is also about 1.5x faster then the generic one, where the 16 variant seems to be not better than the 13 variant.

Additionally I also implemented a copying MSB Radix sort algorithm specifically for string sorting. The implementation is from 2024 I just made it compile again and did not spend more time with it to check if there are some bottlenecks I can avoid. The benchmark from 2024 shows that std sort is almost always faster than the radix sort by about 2x.

This is what I currently have and now comes what I need to do after I watched the talk linked above.

I need to implement American Flag sort which is an in place variant of MSB Radix sort (in place means no additional temp memory allocation, only a stack allocation for the histogram). Then compare it to my copying Radix sort implementation.

Next look at the Ska sort implementation, from the speaker of the talk and implement this. His implementation is more generic, allowing to provide the algorithm with partitioning value if you will. I need to study how he does it and if it is applicable in current state of Mojo.

The generalization effort is kind of orthogonal to the sorting algorithm itself.

One other thing I’d like to see the primitive used for is that I’ve seen radix sort used to minimize the amount of comparisons of another algorithm by sorting each of the buckets using a different key function or by making each bucket a heap. This can also help cut down on the number of buckets.

@owenhilyard could you point me to this algorithms. Until now I see optimizations which go toward increasing the number of buckets instead of reduction, this would be an interesting avenue to explore.

As always, sorting turns out to be quite a rabbit hole.

[owenhilyard]

The general algorithm is that you radix sort to get things into other buffers, then do something like a quicksort inside of those buckets. This lets you avoid needing to do a more expensive sort on a large number of items while also letting you avoid needing to make more than some set of buckets. Once each bucket is sorted then you can iterate the buckets in order and copy the items into the output list. This can save a lot of compares without invoking all of the requirements of radix sorting everything. It works especially know if you have a good idea of the distribution of input data and can adjust the bucket ranges to match.

I like to use it for strings since it lets me get away with fewer compares and if each bucket is a heap then the sort is still O(n log n) even with having to do a lot of heap adds and removals, but it’s a better absolute complexity since you’re subdividing the heaps.

[mzaks (Maxim)]

So I implemented American flag sort (aflag), with some optimizations. I also implemented MSB Radix sort for Scalars (called it aflag_copy sorry for the terrible naming).

All in all in my benchmarks LSB Radix is still the most performant option. AFlag is actually not that great, it sometimes outperforms the std sort, but it is no match to LSB or MSB Radix.

Regarding generalization, MSB Radix sort can be generalized. IMHO it would be best done with a trait MSBPratitionable which will return a UInt8 or even SIMD[DType.uint8, width] (to allow some optimizations in regards of histogram computation) for a certain depth.

So something like

trait MSBPratitionable:
    fn partition(self, level: Int) -> UInt8

trait MSBPratitionableByFour:
    fn partition(self, level: Int) -> SIMD[DType.uint8, 4]

The benchmark results can be found here:

scalar_large_report_zen5.csv

and here:

scalar_large_report_m4.csv

Would appreciate another set of eyes on AFlag sort implementation.

radix_sorting/aflag.mojo

[mzaks (Maxim)]

A diagram tells more than 1000 words so here we go.

Plotted results of different sorting algorithms benchmarked on MacBookPro M4 Max.

The plot for std lib sort, which is a mix of insertion sort and quick sort (so an in-place unstable sort):

On the X Axis we have a cross product of lists of different DTypes - UInt8, Int8, UInt16, Int16, Float16, BFloat16, UInt32, Int32, Float32, UInt64, Int64, Float64 and list sizes. 4096, 65536, 1048576.

On the Y Axis we see the number of nano seconds it took on average per element in the list.

Here is a plot for American flag sort, which is also an in-place and un stable sort algorithm. In American flag sort we do need additional memory for histogram computation which is reserved on the stack and is 256 elements of UInt32 and a list of partitions to do recursion on which is 256 elements of UInt8. The Aflag algorithm switches to std lib sort when the partition size is smaller than 256.

Next up is the MSB Radix sort which I called internally copying American flag. This algorithm is unstable and not in place. Additionally to stack allocation we have in American flag, we also need a buffer for copying. We allocate a buffer of same size as the list we need to sort and reuse it in further recursions.

Now comes the LSB Radix sort, which is a stable not in place algorithm. The implementation is unrolled and creates a temporary out list for each level. (It is imaginable to try out reusing single allocation as we did in copying American flag sort.)

Last but not least, we have two micro optimized LSB Radix sort implementation which use 11bit histogram for 32 bit numbers and 13bit histogram for 64 bit numbers. As already mentioned above this implementation is based on stereopsis : graphics : radix tricks and provides additional speed up for the generic LSB Radix sort

[owenhilyard]

These all look great and I think we can expand type support over time. My main request is that you explain the algorithms a bit and annotate the time complexity when merging into the stdlib, in addition to letting people pass in scratch memory so that we don’t have to allocate as part of this. I’d also ideally like a short “guide to choosing a sorting algorithm” that explains the differences between the different radix sort and flag sort variants.